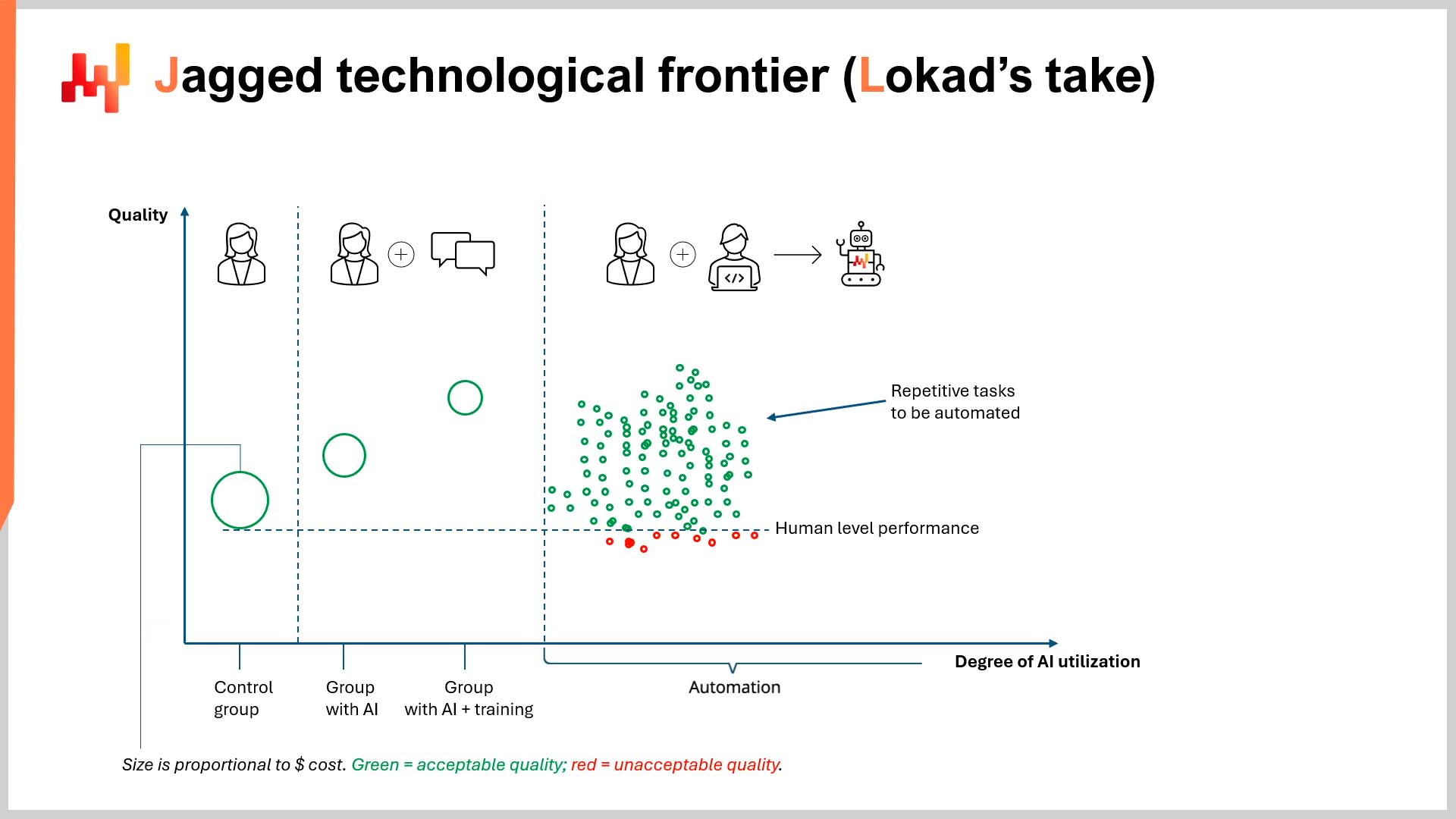
RFI, RFP and RFQ madness in supply chain
Over the years, Lokad has gained some notoriety, and we have earned the privilege of being part of an increasingly large number of RFI (request for information), RFP (request for proposal) and RFP (request for quote) related to supply chain optimization.